>알고리즘 문제
1. 연속 펄스 부분 수열의 합
1)문제
어떤 수열의 연속 부분 수열에 같은 길이의 펄스 수열을 각 원소끼리 곱하여 연속 펄스 부분 수열을 만들려 합니다. 펄스 수열이란 [1, -1, 1, -1 …] 또는 [-1, 1, -1, 1 …] 과 같이 1 또는 -1로 시작하면서 1과 -1이 번갈아 나오는 수열입니다.
예를 들어 수열 [2, 3, -6, 1, 3, -1, 2, 4]의 연속 부분 수열 [3, -6, 1]에 펄스 수열 [1, -1, 1]을 곱하면 연속 펄스 부분수열은 [3, 6, 1]이 됩니다. 또 다른 예시로 연속 부분 수열 [3, -1, 2, 4]에 펄스 수열 [-1, 1, -1, 1]을 곱하면 연속 펄스 부분수열은 [-3, -1, -2, 4]이 됩니다.
정수 수열 sequence가 매개변수로 주어질 때, 연속 펄스 부분 수열의 합 중 가장 큰 것을 return 하도록 solution 함수를 완성해주세요.
제한 사항
- 1 ≤ sequence의 길이 ≤ 500,000
- -100,000 ≤ sequence의 원소 ≤ 100,000
- sequence의 원소는 정수입니다.
2)솔루션
class Solution {
fun solution(sequence: IntArray): Long {
var answer: Long = 0
//카데인 알고리즘 이용
val arr=Array(2){LongArray(sequence.size){0}}
arr[0][0]=sequence[0].toLong()
arr[1][0]=-1L*sequence[0].toLong()
for(i in 1..sequence.size-1){
if(i%2==0){
arr[0][i]=maxOf(sequence[i].toLong(),arr[0][i-1]+sequence[i].toLong())
arr[1][i]=maxOf(sequence[i].toLong()*-1L,arr[1][i-1]+sequence[i].toLong()*-1L)
}else{
arr[0][i]=maxOf(sequence[i].toLong()*-1L,arr[0][i-1]+sequence[i].toLong()*-1L)
arr[1][i]=maxOf(sequence[i].toLong(),arr[1][i-1]+sequence[i].toLong())
}
}
return maxOf(arr[0].maxOrNull()!!,arr[1].maxOrNull()!!)
}
}-DP의 카데인 알고리즘을 활용
<1>원리: fn을 끝 인덱스로 하는 부분합의 최댓값 Sn에 대하여 Sn+1을 구하고자 할시 Sn+fn+1과 fn을 비교해서 더 큰값이 부분함이 되는 것.
<2>증명
S1=f1
S2=max(f2,S1+f2)
=>기존 부분합 최대가 음수면 오히려 더한값이 더 줄어들으므로 f2가 부분합이 최대가 되기도 한다.
.
.
.
Sn=max(fn,S(n-1)+fn)
=>위의 방식을 반복하면 fn을 끝 인덱스로 하는 부분합들의 최대값을 구할 수있다.
2. 산 모양 타일링
1)문제
문제 설명
한 변의 길이가 1인 정삼각형 2n+1개를 이어붙여 윗변의 길이가 n, 아랫변의 길이가 n+1인 사다리꼴을 만들 수 있습니다. 이때 사다리꼴의 윗변과 변을 공유하는 n개의 정삼각형 중 일부의 위쪽에 같은 크기의 정삼각형을 붙여 새로운 모양을 만들었습니다. 예를 들어 n이 4이고, 1번째, 2번째, 4번째 정삼각형 위에 정삼각형을 붙인 모양은 다음과 같습니다.

이렇게 만든 모양을 정삼각형 타일 또는 정삼각형 2개를 이어 붙인 마름모 타일로 빈 곳이 없도록 채우려고 합니다. 정삼각형 타일과 마름모 타일은 돌려서 사용할 수 있습니다.

타일을 놓을 때 다른 타일과 겹치거나 모양을 벗어나게 놓을 수는 없습니다. 위의 예시 모양을 채우는 방법 중 일부는 다음과 같습니다.
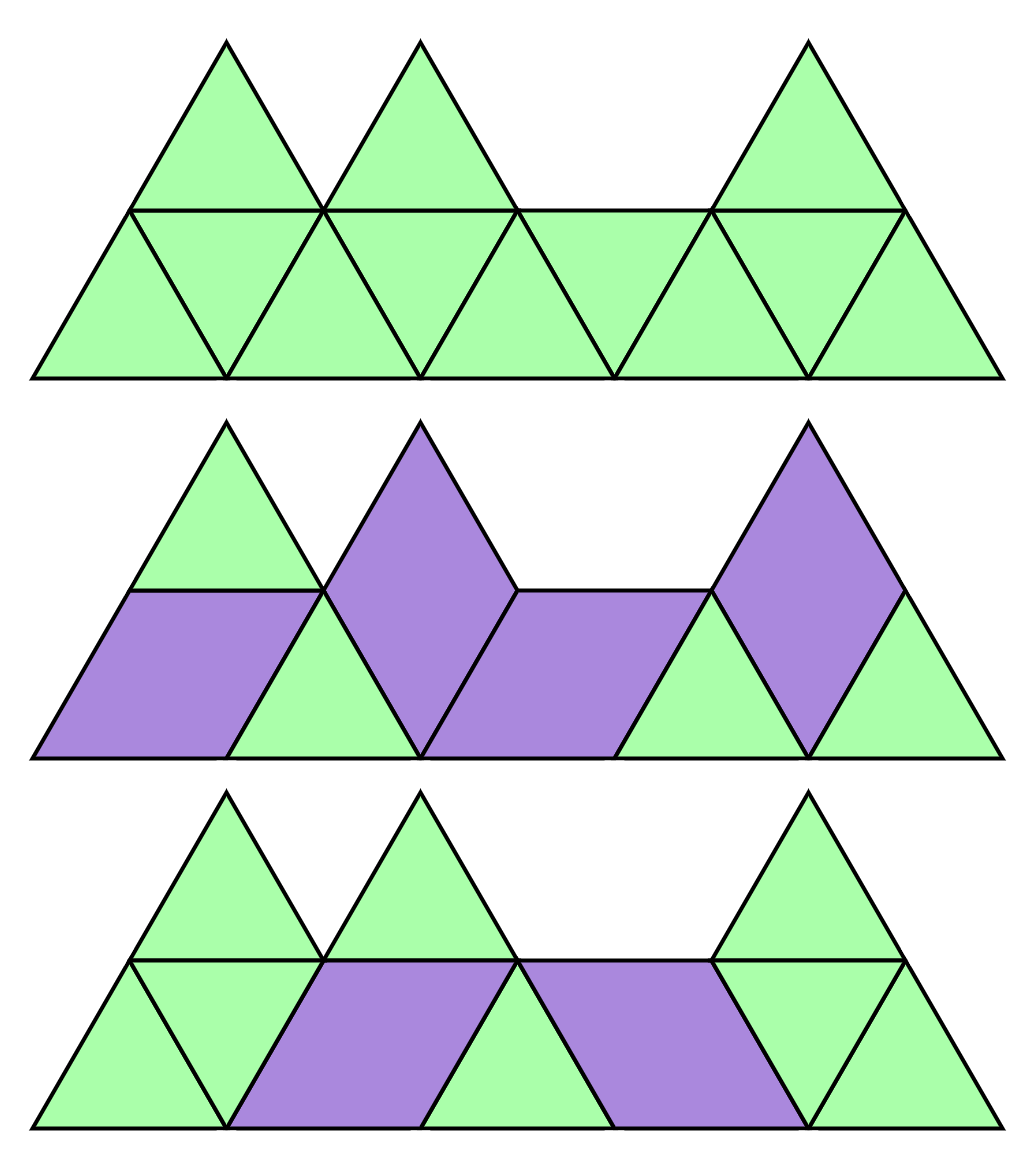
사다리꼴의 윗변의 길이를 나타내는 정수 n과 사다리꼴 윗변에 붙인 정삼각형을 나타내는 1차원 정수 배열 tops가 매개변수로 주어집니다. 이때 문제 설명에 따라 만든 모양을 정삼각형 또는 마름모 타일로 빈 곳이 없도록 채우는 경우의 수를 10007로 나눈 나머지를 return 하도록 solution 함수를 완성해 주세요.
제한사항
- 1 ≤ n ≤ 100,000
- tops의 길이 = n
- tops[i]는 사다리꼴의 윗변과 변을 공유하는 i+1번째 정삼각형의 위쪽에 정삼각형을 붙이는 경우 1, 붙이지 않는 경우 0입니다.
2)솔루션
class Solution {
fun solution(n: Int, tops: IntArray): Int {
//우하단 칠하는 경우에(사각형으로 채우는 경우) 따라 나누어 구함
//tri[i][0]가 안칠한 경우, tri[i][1]이 칠한 경우일시
val tri=Array(n){IntArray(2){0}}
tri[0][1]=1
tri[0][0]=if(tops[0]==1) 3 else 2
for(i in 1..n-1){
if(tops[i]==1){
tri[i][0]=(3*tri[i-1][0]+2*tri[i-1][1])%10007
}else{
tri[i][0]=(2*tri[i-1][0]+tri[i-1][1])%10007
}
tri[i][1]=(tri[i-1][0]+tri[i-1][1])%10007
}
return (tri[n-1][0]+tri[n-1][1])%10007
}
}-4개 삼각형으로 이루어진 삼각형(혹은 3개삼각형으로 이루어진 사다리꼴) 단위로 나누어 계산
-우하단이 칠해지는지 여부에 따라 tri[i][0]은 i번째에서 우하단에 삼각형이 칠해지지 않는 경우(즉 사각형으로 채우는 경우) 경우의수 총합이고 tri[i][1]은 i번째에서 우하단 삼각형이 칠해지는 경우 경우의수 총합
3. 상담원 인원
1)문제
현대모비스는 우수한 SW 인재 채용을 위해 상시로 채용 설명회를 진행하고 있습니다. 채용 설명회에서는 채용과 관련된 상담을 원하는 참가자에게 멘토와 1:1로 상담할 수 있는 기회를 제공합니다. 채용 설명회에는 멘토 n명이 있으며, 1~k번으로 분류되는 상담 유형이 있습니다. 각 멘토는 k개의 상담 유형 중 하나만 담당할 수 있습니다. 멘토는 자신이 담당하는 유형의 상담만 가능하며, 다른 유형의 상담은 불가능합니다. 멘토는 동시에 참가자 한 명과만 상담 가능하며, 상담 시간은 정확히 참가자가 요청한 시간만큼 걸립니다.
참가자가 상담 요청을 하면 아래와 같은 규칙대로 상담을 진행합니다.
- 상담을 원하는 참가자가 상담 요청을 했을 때, 참가자의 상담 유형을 담당하는 멘토 중 상담 중이 아닌 멘토와 상담을 시작합니다.
- 만약 참가자의 상담 유형을 담당하는 멘토가 모두 상담 중이라면, 자신의 차례가 올 때까지 기다립니다. 참가자가 기다린 시간은 참가자가 상담 요청했을 때부터 멘토와 상담을 시작할 때까지의 시간입니다.
- 모든 멘토는 상담이 끝났을 때 자신의 상담 유형의 상담을 받기 위해 기다리고 있는 참가자가 있으면 즉시 상담을 시작합니다. 이때, 먼저 상담 요청한 참가자가 우선됩니다.
참가자의 상담 요청 정보가 주어질 때, 참가자가 상담을 요청했을 때부터 상담을 시작하기까지 기다린 시간의 합이 최소가 되도록 각 상담 유형별로 멘토 인원을 정하려 합니다. 단, 각 유형별로 멘토 인원이 적어도 한 명 이상이어야 합니다.
예를 들어, 5명의 멘토가 있고 1~3번의 3가지 상담 유형이 있을 때 아래와 같은 참가자의 상담 요청이 있습니다.
참가자의 상담 요청
참가자 번호시각상담 시간상담 유형
| 1번 참가자 | 10분 | 60분 | 1번 유형 |
| 2번 참가자 | 15분 | 100분 | 3번 유형 |
| 3번 참가자 | 20분 | 30분 | 1번 유형 |
| 4번 참가자 | 30분 | 50분 | 3번 유형 |
| 5번 참가자 | 50분 | 40분 | 1번 유형 |
| 6번 참가자 | 60분 | 30분 | 2번 유형 |
| 7번 참가자 | 65분 | 30분 | 1번 유형 |
| 8번 참가자 | 70분 | 100분 | 2번 유형 |
이때, 멘토 인원을 아래와 같이 정하면, 참가자가 기다린 시간의 합이 25로 최소가 됩니다.
1번 유형2번 유형3번 유형
| 2명 | 1명 | 2명 |
1번 유형
1번 유형을 담당하는 멘토가 2명 있습니다.
- 1번 참가자가 상담 요청했을 때, 멘토#1과 10분~70분 동안 상담을 합니다.
- 3번 참가자가 상담 요청했을 때, 멘토#2와 20분~50분 동안 상담을 합니다.
- 5번 참가자가 상담 요청했을 때, 멘토#2와 50분~90분 동안 상담을 합니다.
- 7번 참가자가 상담 요청했을 때, 모든 멘토가 상담 중이므로 1번 참가자의 상담이 끝날 때까지 5분 동안 기다리고 멘토#1과 70분~100분 동안 상담을 합니다.
2번 유형
2번 유형을 담당하는 멘토가 1명 있습니다.
- 6번 참가자가 상담 요청했을 때, 멘토와 60분~90분 동안 상담을 합니다.
- 8번 참가자가 상담 요청했을 때, 모든 멘토가 상담 중이므로 6번 참가자의 상담이 끝날 때까지 20분 동안 기다리고 90분~190분 동안 상담을 합니다.
3번 유형
3번 유형을 담당하는 멘토가 2명 있습니다.
- 2번 참가자가 상담 요청했을 때, 멘토#1과 15분~115분 동안 상담을 합니다.
- 4번 참가자가 상담 요청했을 때, 멘토#2와 30분~80분 동안 상담을 합니다.
상담 유형의 수를 나타내는 정수 k, 멘토의 수를 나타내는 정수 n과 참가자의 상담 요청을 담은 2차원 정수 배열 reqs가 매개변수로 주어집니다. 멘토 인원을 적절히 배정했을 때 참가자들이 상담을 받기까지 기다린 시간을 모두 합한 값의 최솟값을 return 하도록 solution 함수를 완성해 주세요.
제한사항
- 1 ≤ k ≤ 5
- k ≤ n ≤ 20
- 3 ≤ reqs의 길이 ≤ 300
- reqs의 원소는 [a, b, c] 형태의 길이가 3인 정수 배열이며, c번 유형의 상담을 원하는 참가자가 a분에 b분 동안의 상담을 요청했음을 의미합니다.
- 1 ≤ a ≤ 1,000
- 1 ≤ b ≤ 100
- 1 ≤ c ≤ k
- reqs는 a를 기준으로 오름차순으로 정렬되어 있습니다.
- reqs 배열에서 a는 중복되지 않습니다. 즉, 참가자가 상담 요청한 시각은 모두 다릅니다.
2)솔루션
class Solution {
fun solution(k: Int, n: Int, reqs: Array<IntArray>): Int {
var answer: Int = 0
var mentor=IntArray(k+1){1}
while(mentor.sum()<=n){
var min=Int.MAX_VALUE
var minIdx=0
for(i in 1..k){
var tmp=mentor.copyOf()
tmp[i]++
var tmptime=waitTime(tmp,reqs,k)
if(min>tmptime){
min=tmptime
minIdx=i
}
}
mentor[minIdx]++
}
return waitTime(mentor,reqs,k)
}
fun waitTime(men:IntArray, reqs:Array<IntArray>, k:Int ):Int{
var time=0
for(i in 1..k){
val mens=men[i]
val arr=IntArray(mens){0}
for(j in reqs){
if(j[2]==i){
var min=arr.minOrNull() as Int
val minIdx=arr.indexOf(min)
min=maxOf(min,j[0])
time+=maxOf(0,min-j[0])
arr[minIdx]=min+j[1]
}
}
}
println(men.contentToString())
println(time)
return time
}
}-유형별로 한명씩 추가해 보면서 그중 시간이 가장 적게 드는 쪽에 상담원을 배치하는 식으로 반복해서 결과를 찾는다.
4. n^2 배열 자르기
1)문제
정수 n, left, right가 주어집니다. 다음 과정을 거쳐서 1차원 배열을 만들고자 합니다.
- n행 n열 크기의 비어있는 2차원 배열을 만듭니다.
- i = 1, 2, 3, ..., n에 대해서, 다음 과정을 반복합니다.
- 1행 1열부터 i행 i열까지의 영역 내의 모든 빈 칸을 숫자 i로 채웁니다.
- 1행, 2행, ..., n행을 잘라내어 모두 이어붙인 새로운 1차원 배열을 만듭니다.
- 새로운 1차원 배열을 arr이라 할 때, arr[left], arr[left+1], ..., arr[right]만 남기고 나머지는 지웁니다.
정수 n, left, right가 매개변수로 주어집니다. 주어진 과정대로 만들어진 1차원 배열을 return 하도록 solution 함수를 완성해주세요.
제한사항
- 1 ≤ n ≤ 107
- 0 ≤ left ≤ right < n2
- right - left < 105
2)솔루션
class Solution {
fun solution(n: Int, left: Long, right: Long): IntArray {
var answer: IntArray = intArrayOf()
for(i in left..right){
answer+=if(i/n.toLong()>=i%n.toLong()){
(i/n.toLong() + 1L).toInt()
}else{
(i%n.toLong() + 1L).toInt()
}
}
return answer
}
}-인덱스 i에 대해 배열 값이 어떻게 나오는지 계산해서 left에서 right사이 인덱스만 체크해 답이 나오도록 함
>입문강의 4주차
1. 액티비티
1)안드로이드 4대 컴포넌트
<1>액티비티: 사용자와 직접 상호작용, UI담당
<2>서비스: 백그라운드에서 오랜시간 실행되어야하는 작업 수행(ex-음악 재생, 파일 다운로드)
<3>브로드캐스트 리시버: 안드로이드 시스템으로 부터 다양한 이벤트나 정보를 앱이 받을 수 있게 해주는 컴포넌트(ex-배터리 부족, 화면꺼짐등)
<4>콘텐드 프로바이더: 앱간 데이터 공유를 가능하게 함. 일종의 데이터베이스 역할(ex-연락처 앱이 연락처 데이터를 다른 앱에 제공)
2)액티비티와 사용자 인터페이스 연결:setContentView(아이디)
2. 인텐트
1)인텐트란: 다른 앱 구성요소(액티비티, 서비스, 브로드캐스트 리시버)에 작업 요청 가능
2)종류
<1>명시적 인텐트: 시작할 구성요소의 이름을 인텐트 객체에 설정하고 실행시키는것
=>예시:
val intent=Intent(this, AnotherActivity::class.java)<2>암시적 인텐트: :시작할 구성요소 이름을 지정하지않고 일반적인 작업(전화걸기,지도보기,인터넷창 띄우기등)을 인텐트 객체에 설정해 실행
=>안드로이드 시스템이 모든 앱을 검색해 해당 인텐트와 일치하는 인텐트 필터를 찾고 일치된 인텐트 필터로 앱을 시작시킴
=>예시:
val callIntent=Intent(Intent.ACTION_DIAL, Uri.parse("tel:114"))
@인텐트 필터: 특정 인텐트에 반응하는 액티비티,서비스 또는 브로드캐스트 리시버의 능력. 인텐트를 수신할 준비가 되어있는지 나타냄
=>예를 들어 파일 뷰어 앱을 제작하고 인텐트 필터에 파일 뷰어 기능을 가졌다고 설정해 두면 인텐트가 실행됐을때 불러와질 수도 있음
@onClick속성 이용 방법: 여러 버튼이 동일 onClick속성값을 갖는 경우
=>view.id로 어느 버튼이 누른것인지 식별해서 실행
=>예시
fun doOnClick(view: View){
when(view.id){
R.id.btn3->{
val callIntent=Intent(Intent.ACTION_DIAL, Uri.parse("tel:114"))
startActivity(callIntent)
}
R.id.btn4->{
val mapIntent=Intent(Intent.ACTION_VIEW, Uri.parse("geo:37.565350, 127.01445"))
startActivity(mapIntent)
}
}
}
3)인텐트 구성
<1>컴포넌트 이름: Intent(context, TargetActivity::class.java)에서 TargetActivity에 해당
=>컴포넌트 이름이 없으면 암시적 인텐트로 처리됨
<2>액션: 암시적 인텐트에서 어떤 동작을 할지에 해당
-Intent.ACTION_VIEW: 사용자에게 데이터를 보여줌
-Intent.ACTION_DIAL: 전화 다이얼을 열기위해 사용
<3>데이터: 암시적 인텐트에서 작업수행에 필요한 데이터를 "URI"로 지정
=>예시:다이얼의 경우 Uri.parse("tel:12312412") 의 형태
<4>카테고리:
-인텐트 필터에서 사용
<activity android:name=".SecondActivity">
<intent-filter>
<action android:name="android.intent.action.MAIN" />
<category android:name="android.intent.category.LAUNCHER" />
</intent-filter>
</activity>=>이 경우 앱 실행시 위 액티비티가 먼저 실행됨
-암시적 인텐트에 카테고리 추가
intent.addCategory(Intent.CATEGORY_BROWSABLE)이와 같이 카테고리 추가 가능
<5>엑스트라
-데이터를 인텐트로 전달하기 위한 키-값 쌍의 정보
-전달: 아래방식으로 기본데이터(boolean, byte~long,float,double,char), String, Serializable, Parcelable, 배열, bundle
@Serializable과 Parcelable의 경우 인터페이스로 클래스가 해당 인터페이스를 상속받으면 인텐트로 인스턴스 전달가능
=>성능면에서 Parcelable이 좋음
-ArrayList의 경우 putIntegerArrayListExtra()처럼 형식이 다름
intent.putExtra("key", "value")@자바는 intent를 getIntent로 받아야 하는것과 달리 코틀린은 그냥 바로 intent로 쓰면 된다.
-수신: 수신 정보의 타입에 따라 다름(String, 기본데이터, Serializable, Parcelable, 배열은 "타입Array"로)
intent.get타입Extra("key")
3)인텐트 필터
<1>manifest에서 acitivity내에 작성
<2> 특정 인텐트에 대해 작업이 실행될 수 있도록 해줌
@인텐트 필터로 액티비티가 불러와 지려면 exported는 true이어야 한다.(안 적어두면 디폴트가 true임)
<3>예시
<activity android:name=".SecondActivity"
android:label="Second Activity"
android:exported="true">
<!--추가된 인텐트 필터 시작-->
<intent-filter>
<action android:name="android.intent.action.DIAL" />
<category android:name="android.intent.category.DEFAULT" />
<data android:scheme="tel" />
</intent-filter>
<!--추가된 인텐트 필터 끝-->
</activity>
@android:label
-application에서의 라벨:설치 삭제시 뜨는 앱이름
-activity에서의 라벨:설치된 앱의 이름=>이건 없어도 되지만 인텐트 필터에서 통과된 구성요소가 하나 이상인 경우 android:label을 이름으로 해서 선택지가 나열되므로 인텐트 필터가 있는 액티비티에서는 라벨이 있는게 좋음(액티비티 구분용)
=>없으면 application의 android:label이 기본값으로 사용됨
3. 액티비티 생명주기

1)화면에 보이는 구간: onStart() ~ onStop()
-다른 액티비티로 넘어갈 경우 기존 액티비티는 onStop()으로 갔다가 다시 돌아오면 onRestart()로 onStart()에 간다
2)foreground에서 동작하는 구간: onResume() ~ onPause()
-홈키로 잠시 앱을 내리거나 다이얼로그가 화면위로 뜨면 onPause() 다시 돌아오면 onResume()
3)각 생명주기별 콜백 메소드
-생명주기별로 실행되는 메소드를 오버라이드해서 사용할 수 있음
-블럭 내, super~아래부분에 작성하면 된다.
override fun onStart() {
super.onStart()
}
override fun onResume() {
super.onResume()
}
override fun onPause() {
super.onPause()
}
override fun onStop() {
super.onStop()
}
override fun onRestart() {
super.onRestart()
}
override fun onDestroy() {
super.onDestroy()
}
>개인과제-로그인 앱 만들기
'코틀린-안드로이드' 카테고리의 다른 글
| 28일차)알고리즘 문제(할인 행사) (2) | 2024.06.21 |
|---|---|
| 27일차)알고리즘 문제(행렬의 곱셈, 표 병합, 표현 가능한 이진트리, 부대복귀) (0) | 2024.06.20 |
| 25일차)알고리즘 문제(연속 부분 수열 합의 개수, H-Index, 인사고과), 입문 강의 1~3주차 (1) | 2024.06.18 |
| 24일차)알고리즘 문제(고고학 최고의 발견, n + 1 카드게임, 귤 고르기, 괄호 회전하기) (1) | 2024.06.16 |
| 23일차)알고리즘 문제(멀리 뛰기, 에어컨, 아방가르드 타일링, 숫자 타자 대회) (1) | 2024.06.14 |
